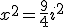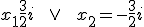Materiały » Zadania 


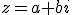 , gdzie
, gdzie 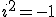 . Wartość a nazywamy rzeczywistą, a wartość b urojoną. Dzięki stosowaniu liczb zespolonych można rozwiązywać wiele równań, które nie mają rozwiązania w zbiorze liczb rzeczywistych. Równanie
. Wartość a nazywamy rzeczywistą, a wartość b urojoną. Dzięki stosowaniu liczb zespolonych można rozwiązywać wiele równań, które nie mają rozwiązania w zbiorze liczb rzeczywistych. Równanie 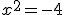 w zbiorze R nie ma rozwiązań, ale gdy zastosujemy liczby zespolone (podstawiając za -1 liczbę
w zbiorze R nie ma rozwiązań, ale gdy zastosujemy liczby zespolone (podstawiając za -1 liczbę 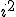 ), to otrzymamy
), to otrzymamy 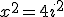 , a takie równie ma rozwiązania urojone:
, a takie równie ma rozwiązania urojone: 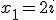 oraz
oraz 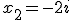 . Równanie
. Równanie 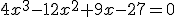 ma:
ma:
Pokaż rozwiązanie »





Zadanie 206
Liczby zespolone mają postać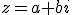 , gdzie
, gdzie 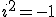 . Wartość a nazywamy rzeczywistą, a wartość b urojoną. Dzięki stosowaniu liczb zespolonych można rozwiązywać wiele równań, które nie mają rozwiązania w zbiorze liczb rzeczywistych. Równanie
. Wartość a nazywamy rzeczywistą, a wartość b urojoną. Dzięki stosowaniu liczb zespolonych można rozwiązywać wiele równań, które nie mają rozwiązania w zbiorze liczb rzeczywistych. Równanie 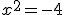 w zbiorze R nie ma rozwiązań, ale gdy zastosujemy liczby zespolone (podstawiając za -1 liczbę
w zbiorze R nie ma rozwiązań, ale gdy zastosujemy liczby zespolone (podstawiając za -1 liczbę 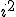 ), to otrzymamy
), to otrzymamy 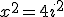 , a takie równie ma rozwiązania urojone:
, a takie równie ma rozwiązania urojone: 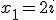 oraz
oraz 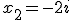 . Równanie
. Równanie 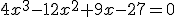 ma:
ma:
| TAK | NIE | ||
| A. 3 rozwiązania rzeczywiste | |||
| B. 2 rozwiązania rzeczywiste i jedno urojone | |||
C. tylko rozwiązanie 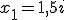 | |||
D. rozwiązania: 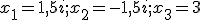 |
Pokaż rozwiązanie »






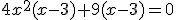
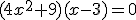

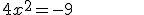 rozwiązanie rzeczywiste
rozwiązanie rzeczywiste