WSTĘP

W lekcji zajmiemy się podzielnością liczb. Na pewno wiesz, że cyfra 4 dzieli się przez 2, cyfra 6 dzieli się przez 3, liczba 12 dzieli się przez 4, ale co zrobić z liczbą większą, np. 34584042905, kiedy chcemy sprawdzić czy jest podzielna na przykład przez 5, ale nie potrzebujemy znać wyniku? Czy bez pomocy kalkulatora będziemy umieli sobie z nią poradzić? Po dzisiejszej lekcji na pewno bez problemu.

Zapoznacie się w lekcji z zasadami, które mówią, kiedy liczba jest podzielna przez inną. Na początek przypomnimy sobie zasady dla podzielności przez liczby od 2 do 10, a później poznamy również bardziej rozbudowane zasady dotyczące podzielności przez 7, 11 oraz 13.

Pamiętaj, że zadania dotyczące podzielności liczb bardzo często występują na konkursach, dlatego warto zapamiętać kilka prostych zasad. Jeśli będziesz ich używać z łatwością zapamiętasz je wszystkie. 

CO TO ZNACZY, ŻE LICZBA JEST PODZIELNA PRZEZ INNĄ LICZBĘ?

Jeżeli liczba "a" jest podzielna przez liczbę "b", to oznacza, że dzieląc liczbę "a" przez liczbę "b" nie zostaje nam żadna reszta (czyli reszta równa się zero). Mówimy wtedy, że liczba "b" jest dzielnikiem liczby "a".

ZASADY PODZIELNOŚCI PRZEZ LICZBY OD 2 DO 10

Omówimy teraz poszczególne zasady podzielności, a pomoże nam w tym poniższa plansza.

Cechy podzielności przez liczby od 2 do 10

Jeżeli chcesz sprawdzić czy dana liczba ma dzielniki z zakresu od 2 do 10, możesz skorzystać z planszy interaktywnej. Warto o niej pamiętać przy rozwiązywaniu zadań, żeby móc sprawdzić swoje obliczenia.

PODZIELNOŚĆ PRZEZ 2

Liczba będzie podzielna przez 2, jeżeli na końcu tej liczby będzie stała któraś z następujących cyfr:0, 2, 4, 6, 8. Nie jest ważne jakie cyfry są wcześniej, interesuje nas tylko ostatnia cyfra.

Przykłady liczb:

20, 552, 7894, 95736, 678368

PODZIELNOŚĆ PRZEZ 3

Liczba będzie podzielna przez 3, jeżeli suma wszystkich cyfr tej liczby jest podzielna przez 3.

Przykłady liczb:

1110, ponieważ 1+1+1+0=3, a wiemy, że każda liczba dzieli się przez samą siebie, więc 3 również dzieli się przez 3

2403, ponieważ 2+4+0+3=9, a wiemy, że 9 dzieli się przez 3

613110, ponieważ 6+1+3+1+1+0=12, a wiemy, że 12 dzieli się przez 3

PODZIELNOŚĆ PRZEZ 4

Liczba będzie podzielna przez 4, jeżeli liczba złożona z dwóch ostatnich cyfr jest podzielna przez 4. Tutaj również nie interesują na cyfry wcześniejsze, sprawdzamy tylko dwie ostatnie.

Przykłady liczb:

345678912, ponieważ 12 dzieli się przez 4

45604, w takim przypadku rozpatrujemy tylko ostatnią cyfrę, czyli 4 dzieli się przez 4

90875640, ponieważ 40 dzieli się przez 4

PODZIELNOŚĆ PRZEZ 5

Liczba będzie podzielna przez 5, jeżeli na końcu tej liczby będzie stała cyfra 0 lub 5.

Przykłady liczb:

45, 988540, 567324565

PODZIELNOŚĆ PRZEZ 6

Liczba będzie podzielna przez 6, jeżeli jest podzielna jednocześnie przez 2 i przez 3. Oznacza to, że musimy sprawdzić dwie zasady i obie muszą być spełnione.

Przykłady liczb:

7452132, ponieważ 7+4+5+2+1+3+2= 24, więc dzieli się przez 3, a dodatkowo ostatnia cyfra tej liczby to 2, więc obie zasady są spełnione

435051 - nie jest podzielna przez 6, ponieważ chociaż 4+3+5+0+5+1=18, co dzieli się przez 3, to na ostatnim miejscu znajduje się cyfra 1, więc nie jest spełniona zasada podzielności przez 2

PODZIELNOŚĆ PRZEZ 9

Liczba będzie podzielna przez 9, jeżeli suma wszystkich cyfr tej liczby jest podzielna przez 9. Zauważ, że ta zasada jest podobna do zasady podzielności przez 3, z tym, że suma musi być podzielna przez 9.

Przykłady liczb:

303021, ponieważ 3+0+3+0+2+1=9, a wiemy, że liczba 9 jest podzielna przez samą siebie, czyli przez 9

5416317, ponieważ 5+4+1+6+3+1+7=27, a wiemy, że 27 dzieli się przez 9

ZASADA PODZIELNOŚCI PRZEZ 7, 11, 13

Oprócz cech podzielności przypomnianych powyżej można jeszcze wyróżnić kilka innych zasad, bardzo często wykorzystywanych w zadaniach konkursowych.  Wśród nich są zasady podzielności przez 7,11 oraz 13.

Korzystając z plansz poniżej zapoznaj się z zasadami, w jaki sposób możemy zbadać czy liczba jest podzielna przez 7, 11 lub 13.

Dodatkowo przy podzielności przez 7 oraz 11 możesz skorzystać z plansz interaktywnych, w których po wpisaniu liczby uzyskasz odpowiedź czy jest ona podzielna przez 7 lub 11.

Cecha podzielności przez 7

Cecha podzielności przez 7.

Dariusz Kulma - Matematyka innego wymiaru, Utworzony z GeoGebra

Cecha podzielności przez 11

Cecha podzielności przez 13

WŁASNOŚĆ

Jeżeli każdy składnik sumy jest podzielny przez pewną liczbę, to również suma jest podzielna przez tę liczbę.

Sprawdżmy to:

Czy suma liczb 18+24+6+3 jest podzielna przez 3?

Wiemy, że każda z tych liczb jest podzielna przez 3, więc musimy sprawdzić czy suma również:

18+24+6+3=51, a z zasad podzielności pamiętamy, że 5+1=6, czyli dzieli się przez 3, więc cała liczba dzieli się przez 3

Czy suma liczb 50+45+20+5+25 jest podzielna przez 5?

Wiemy, że każda z tych liczb jest podzielna przez 5, więc musimy sprawdzić czy suma również:

50+45+20+5+25=145, a z zasad podzielności pamiętamy, że jeżeli na końcu liczby jest 5, to cała liczba jest podzielna przez 5

To jest bardzo przydatna własność, więc warto ją zapamiętać !

WŁASNOŚĆ

Jeżeli w iloczynie jeden czynnik jest podzielny przez daną liczbę, to cały iloczyn jest podzielny przez tę liczbę.

Sprawdżmy to:

Czy iloczyn liczb 12, 5 i 4 jest podzielny przez 6?

Wiemy, że jedna z tych liczb, czyli 12 jest podzielna przez 6. Sprawdźmy więc czy iloczyn też jest podzielny:

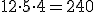, a z zasad podzielności wiemy, że jeżeli liczba jest podzielna przez 2 (na końcu liczby jest zero) i jest również podzielna przez 3 (2+4+0=6), to cała liczba jest podzielna przez 6

Czy iloczyn liczb 20, 3, 2 i 4 jest podzielny przez 10?

Wiemy, że jedna z tych liczb, czyli 20 jest podzielna przez 10. Sprawdźmy więc czy iloczyn też jest podzielny:

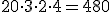, a z zasad podzielności wiemy, że jeżeli liczba ma na końcu zero, to jest podzielna przez 10

ZADANIA Z PORTALU