



Wieża Hanoi
 |
WSTĘPWieżę Hanoi wymyślił francuski matematyk Édouard Lucas dla zabawy w 1883 roku. Édouard Lucas jest również autorem wzoru na n-ty wyraz ciągu Fibonacciego. |
 |
ZASADY GRYWieża składa się z trzech słupków: początkowy, końcowy, pomocniczy (tzw.bufor). Naszym zadaniem jest przenieść wszystkie krążki z początkowego słupka na końcowy z zachowaniem tego samego kształtu wieży, pomagając sobie słupkiem pomocniczym i stosując następujące zasady:
Na początek spróbuj rozwiązać łamigłówkę samodzielnie, wybierając różną ilość krążków. |
GRA - WIEŻA HANOI |
Jeżeli masz problem z ułożeniem krążków, możesz obejrzeć symulację rozwiązania dla poszczególnych ilości krążków, wybierając odpowiednią opcję w grze. |
WZÓR REKURENCYJNYWZÓR REKURENCYJNY na obliczenie ilości potrzebnych ruchów w zależności od ilości krążków: Uzasadnienie wzoru rekurencyjnego: |
 |
WZÓR OGÓLNY: Dowód indukcyjny z wykorzystaniem wzoru rekurencyjnego.Twierdzenie: Dowód:Sprawdzenie dla Istotnie tyle trzeba ruchów do przeniesienia jednopiętrowej wieży, zatem twierdzenie jest prawdziwe dla
Przekształcając wzór rekurencyjny Podstawiając na miejsce
Otrzymaliśmy tezę indukcyjną, więc wzór jest poprawny.
|
LEGENDAJak głosi stara hinduska legenda, przy stworzeniu świata, w jego środku, pod dachem świątyni, umieszczone zostały trzy diamentowe pałeczki. Na jedną z nich nałożonych było 64 złotych krążków o zmniejszających się średnicach tworząc złoty stożek. Dzień i noc, zmieniając się bezustannie, mnisi przekładali krążki na trzecią pałeczkę. Musieli jednak zachować pewne zasady. Mogli posiłkować się drugą pałeczką, jednakże nie wolno było im przenosić więcej niż jeden krążek i umieszczać większego na mniejszym. Gdy wykonają swoje zadanie - nastąpi koniec świata! |
 |
OBLICZMY WIĘC DATĘ KOŃCA ŚWIATA ZGODNIE Z LEGENDĄPodstawiając do wzoru otrzymujemy: |






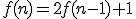
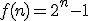
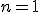
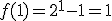
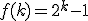
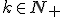
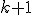
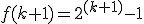
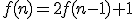 dla
dla 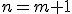 otrzymujemy
otrzymujemy 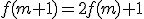
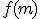 wzór z założenia indukcyjnego otrzymujemy:
wzór z założenia indukcyjnego otrzymujemy: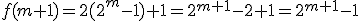
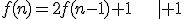
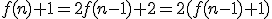
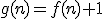
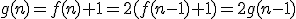
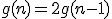
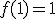 , to
, to 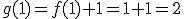
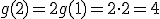
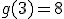
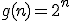
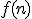 otrzymujemy:
otrzymujemy: 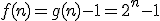
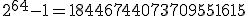 (blisko 18 i pół tryliona) sekund, co daje około 584 542 mld lat, a wszechświat ma około 13,7 mld lat.
(blisko 18 i pół tryliona) sekund, co daje około 584 542 mld lat, a wszechświat ma około 13,7 mld lat.

