



Ciąg Fibonacciego czyli jeszcze o złotej proporcji
Autor
Dariusz Kulma |
WstępHistoria matematyki bywa nieprzewidywalna. Wieki obserwacji i odkryć dotyczących złotej liczby zdawałoby się wyczerpały temat. A jednak nie! A wszystko za sprawą Leonardo Pisano Fibonacciego, który żył w latach ok. 1175 - 1250 n.e. Co ciekawe, nazwisko jest tak naprawdę przydomkiem ,ponieważ Fibonacci znaczy po prosty "syn Bonacciego". Warto dodać, że Fibonacci był gorącym zwolennikiem wprowadzenia arabskiego zapisu liczbowego. |
Fibonacci
|
Wpływ królików na odkrycia matematyczneFibonacci w 1202 roku wydał książkę Liber Abaci (Księga Abaku). Ironiczny tytuł, ponieważ w książce Fibonacci wykazuje korzyści stosowania arabskiego zapisu liczbowego nad metodami opartymi na systemie abaku i cyfrach rzymskich. W książce poruszone są tematy podzielności, teorii liczb, symbolika matematyczna, ale również zasady księgowania, reguły zysków i strat czy wymiany pieniędzy. Jednak najsłynniejszym zadaniem stało się zadanie o królikach. Oto ono: Ile par królików będziemy mieli na końcu roku, jeśli zaczniemy w styczniu z jedną parą królików, ta w każdym następnym miesiącu, poczynając od marca, wyda na świat kolejną parę królików i z każdej pary urodzą się kolejne pary po dwóch miesiącach od narodzin? Jako przesiębiorca i finansista, zamieścił swoje obliczenia w tabeli. Okazało się, że łączna liczba królików w poszczególnych miesiącach tworzyła zadziwiający ciąg liczb. Kolejne liczby były sumą dwóch poprzednich! Zobacz poniższą tabelę z danymi. |
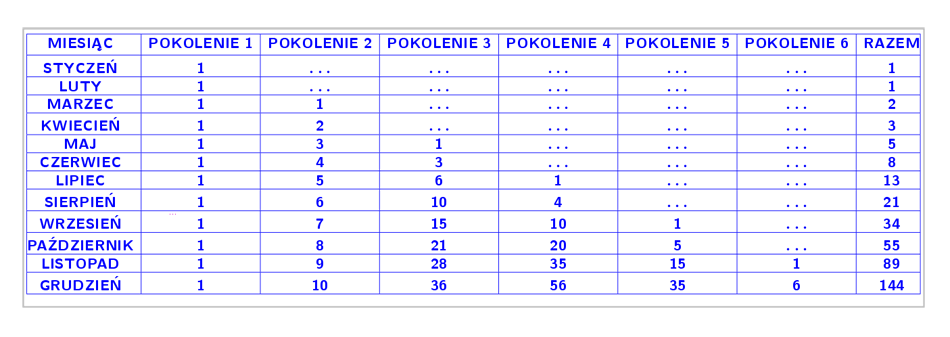 |
Liczby 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,...można tworzyć w nieskończoność. Taki ciąg nazywamy ciągiem rekurencyjnym, gdzie każdy kolejny wyraz zależny jest od poprzednich. Ale gdzie jest tu związek ze złotą liczbą? |
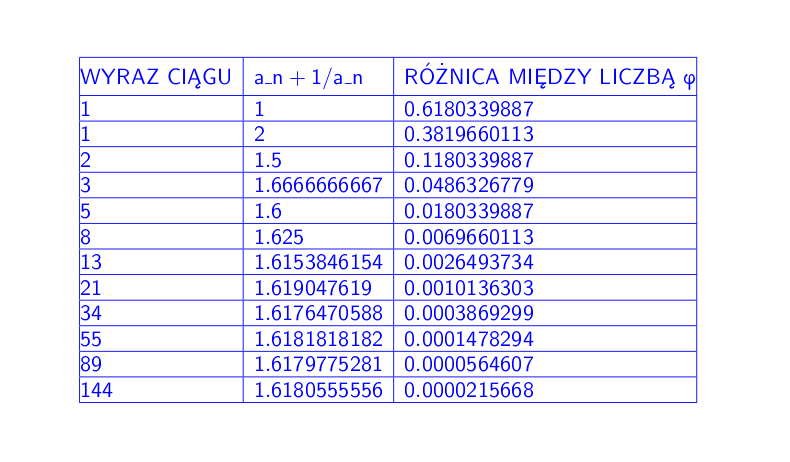
Nieskończenie złoty ciągOkazuje się, że związek ciągu Fibonacciego ze złotą liczbą jest wręcz niebywały. Dzieląc kolejne wyrazy tego ciągu przez wyraz poprzedni otrzymujemy liczby coraz bliższe liczbie zlotej |
 |
Wzór ciągu FibonacciegoCiąg określony jest rekurencyjnie. Są dwa poglądy na to czy ciąg powinien zaczynać się od 0 czy od 1. Biorąc jednak fakt, że ciągi opieramy o liczby naturalne n>0, częściej obserwujemy ciągi zaczynające się od liczby 1. Wzór rekurencyjny może również zawierać wyraz zerowy. Oto wzór: |
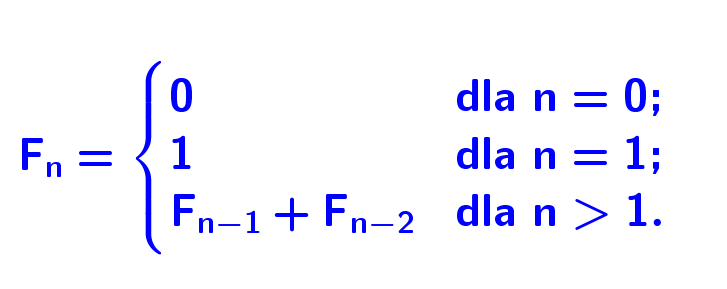 |
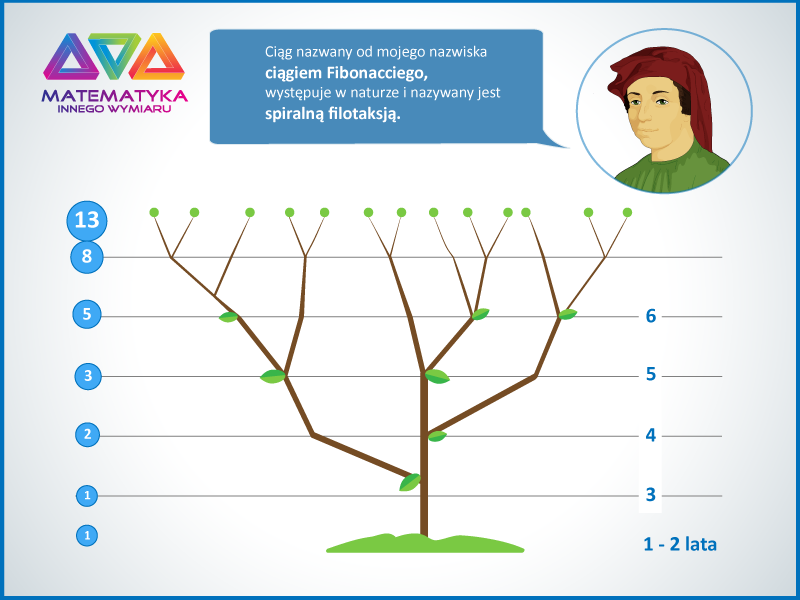
Ciąg Fibonacciego w przyrodzieOkazuje się, że zależność można odnaleźć w przyrodzie. Chociażby ilość kolejnych pędów czy gałęzi drzew albo płatków liścia tworzy ciąg Fibonacciego. |
 |
Złoty prostokąt a spirala FibonacciegoBardzo ciekawą zależnością jest spirala Fibonacciego, która ma bezpośredni związek ze złotym postokątem, czyli takim, którego stosunek długości do szerokości jest w złotym podziale. Przypomnijmy konstrukcję złotego prostokąta. |
Jak już mamy złoty prostokąt, to okazuje się, że gdy zaczniemy rysować łuki o długości promienia, który jest kolejnym wyrazem ciągu Fibonacciego, to otrzymamy spiralę. Obejrzyj animację posługując się planszą interaktywną. |
Spirala FibonacciegoSpirala Fibonacciego Dariusz Kulma - Matematyka innego wymiaru, Utworzony z GeoGebra |
A oto bezpośrednie odniesienie spirali do przyrody. Większość spiralnych muszli opiera się na ciągu Fibonacciego. |
 |







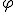 (patrz tabela poniżej). Już dzieląc wyraz trzynasty przez dwunasty mamy błąd rzędu 0.00002. Granicą ciągu Fibonacciego jest więc złota liczba.
(patrz tabela poniżej). Już dzieląc wyraz trzynasty przez dwunasty mamy błąd rzędu 0.00002. Granicą ciągu Fibonacciego jest więc złota liczba.


