MIW Zadania

Równania i nierówności (korelacja z 3 punktem podstawy programowej)

Zadanie 1 - Cztery królewny na noworocznym balu opowiadały sobie, jak dużo miały k...
Zadanie 2 - Równanie $x^{2009}-x^{2008}+x^{2007}-x^{2006}+...-1)(x+1)=0$ ...
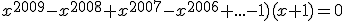Zadanie 3 - Średnia pensja w jednej z firm Kwadratolandii wynosi 2500 dukatów. Pra...
Zadanie 4 - Aby przejechać przez najdłuższy tunel Kwadratolandii, superszybki poci...
Zadanie 5 - 20 mat-owieczek zjadłoby trawę z powierzchni cyfer-łąki w 10 dni. 10 t...
Zadanie 6 - Kwadraty magiczne to takie, które mają identyczną sumę liczb w każdej ...
Zadanie 7 - Siedem sześcian wieków temu w Kwadratolandii panował szalony matematyk...
Zadanie 8 - Wskaż zbiór rozwiązań nierówności: $x\leq \frac{x^2+1}{2}$ ...
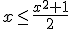Zadanie 9 - Czarny Septylion wymyślił kolejne trudne zadanie, by dręczyć nim swoic...
Zadanie 10 - Różniczka, Matcyfrzak i Dziuglak ważą razem 185 kg. Matcyfrzak, Dziugl...
Zadanie 11 - Czarny Septylion zadał rycerzowi Dwumianusowi do rozwiązania następują...
Zadanie 12 - Dane jest równanie 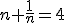$n+\frac{1}{n}=4$ , gdzie $n\in N$ ...
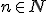Zadanie 13 - Równania, które mają tylko jedno rozwiązanie całkowite, to:...
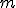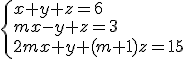Zadanie 14 - Układ równań z parametrem postaci $\begin{cases}x+y+z=6 \\ mx-y+z=3\\2mx+y+(m+1)z=15 \end{cases}$ ...