
Materiały » Zadania 




Potęgi (korelacja z 3 punktem podstawy programowej)
- Zadanie 1 - Rodzice Błyskotki, chcąc pozbyć się jednego z kandydatów do ręki córki...
- Zadanie 2 - Dana jest liczba
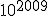 +
+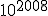 +
+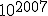 ...
... - Zadanie 3 - Majątek króla Kwadratolandii Pierwiastkusa Wielkiego można przedstawić...
- Zadanie 4 - Jaką cyfrę w rzędzie jedności ma liczba
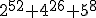 ?...
?... - Zadanie 5 - Dane są liczby:
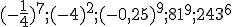 ...
... - Zadanie 6 - W starożytnej Grecji, tak jak teraz w Kwadratolandii, podstawową monet...
- Zadanie 7 - Wyrażenie
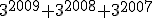 jest podzielne przez:...
jest podzielne przez:... - Zadanie 8 - Liczba
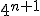 ,dla
,dla 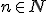 ...
... - Zadanie 9 - Czarny Septylion lubi kamuflować liczby naturalne zmieniając ich posta...
- Zadanie 10 - Komputer Wymierniaka może pomieścić w swej pamięci
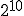 ...
... - Zadanie 11 - Matcyfrzak zapisał liczbę
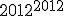 ...
... - Zadanie 12 - Dziuglak obliczał sobie różne palindromiczne potęgi liczb czyli takie,...
- Zadanie 13 - Wymierniak oznaczył liczby
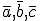 ...
... - Zadanie 14 - Jeśli wyrażeniem
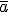 oznaczymy ostatnią cyfrę liczby
oznaczymy ostatnią cyfrę liczby 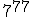 ...
... - Zadanie 15 - Liczba
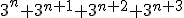 ...
... - Zadanie 16 - Liczba
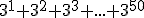 jest podzielna przez:...
jest podzielna przez:... - Zadanie 17 - Liczba
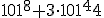 jest podzielna przez:...
jest podzielna przez:...



