



Graniastosłupy prawidłowe
Autor
Dariusz KulmaWstępGraniastosłup nazywamy prawidłowym wtedy, gdy w jego podstawach znajdują się figury foremne czyli takie, które mają wszystkie boki i kąty równe. Ściany boczne takich graniastosłupów są prostokątami. Taki rodzaj graniastosłupów zaliczamy do prostych tzn. mających ściany boczne prostopadłe do podstawy. Nazwę graniastosłupa tworzymy od figury, która znajduje się w podstawie. Jeśli graniastosłup ma w podstawie kwadrat, to nazywamy go graniastosłupem prawidłowym czworokątnym. |
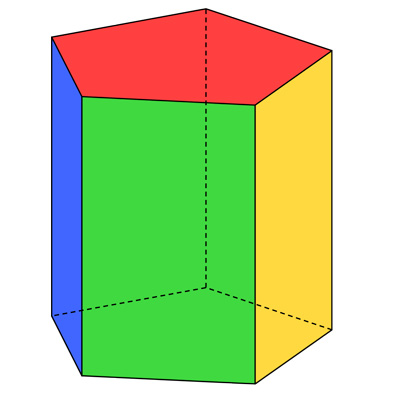 |
Rodzaje graniastosłupówWyświetlaj plansze interaktywne z różnymi graniastosłupami i obserwuj ich własności. Szczególnym przypadkiem graniastosłupa prawidłowego jest sześcian. |
CiekawostkaCiekawym rodzajem brył są antygraniastosłupy. Obejrzyj planszę interaktywną z antygraniastosłupem prawidłowym pięciokątnym i powiedz, czym różni się od graniastosłupów? |
ZADANIA Z PORTALU MIW |
 | Zadanie 556 - W sześcianie o krawędzi 3 cm wydrążono trzy tunele o przekroju kwadrat... |
 | Zadanie 433 - Z siatki na rysunku Dziuglak skleił kostkę. Przyjrzał się uważnie swem... |
 | Zadanie 466 - Nowe akwarium Różniczki ma kształt prostopadłościanu i jest wykonane z... |
 | Zadanie 800 - W szklanym naczyniu w kształcie prostopadłościanu o wymiarach 8 cm × 1... |
 | Zadanie 803 - Siatką prostopadłościanu jest:... |
 | Zadanie 835 - Z siatki poniżej sklejamy kostkę. Następnie wypisujemy liczby trzycyfr... |
 | Zadanie 859 - Podstawą graniastosłupa jest trapez równoramienny, którego ramiona i k... |
 | Zadanie 1201 - Przekątną d prostopadłościanu o krawędziach a, b, c można wyrazić wzor... |
 | Zadanie 1230 - W pięciokącie foremnym o krawędzi 1 każda przekątna ma długość równą z... |
 | Zadanie 1231 - Akwarium w kształcie prostopadłościanu o kwadratowej podstawie i sumi... |









