Wstęp

Kombinatoryka to dział, w którym obliczamy ilość określonych zdarzeń. W tym celu stosujemy 4 najważniejsze kombinatoryczne obliczenia - PERMUTACJE, KOMBINACJE, WARIACJE Z POWTÓRZENIAMI oraz WARIACJE BEZ POWTÓRZEŃ. Samo obliczanie za pomocą określonych wzorów określonej ilości nie jest bardzo skomplikowane. Najważniejszą jednak kwestią jest rozróżnienie, który wzór zastosować do odpowiedniego przykładu. Najlepiej znaleźć takie cechy charakterystyczne, po których będziemy mogli rozróżnić czy zastosować wzór na permutację, kombincję czy którąś z wariacji.

Wskazówka

Oglądając poniżej plansze interaktywne zwróć uwagę w szczególności na cechy charakterystyczne.

PERMUTACJI używamy więc, gdy jednocześnie ustawiamy w różnych kolejnościach wszystkie elementy. Często wykorzystujemy je w zadaniach z ustawianiem ludzi w kolejce, książek na półce, liczb obok siebie itp.

KOMBINACJE to prościej mówiąc losowanie elementów, przy czym kolejność nie jest istotna. LICZY SIĘ EFEKT LOSOWANIA! Nieistotne w jakiej kolejności przyszła dobra karta w grze, ważne, że ją mam. Wybieramy delegację z jakiejś liczby osób i nie ma znaczenia czy jestem wylosowany jako pierwszy czy jako ostatni do delegacji. Ważny jest efekt - jestem w delegacji. Stosujemy je często przy zadaniach z kartami, urnami, losowaniem losów, losowaniem pytań na egzaminie.

WARIACJE Z POWTÓRZENIAMI można dość prosto rozpoznać, jeśli widzimy, że jakieś elementy się powtarzają. Chociażby trzykrotny rzut kostką. Każdy wynik może się powtórzyć 3 razy, więc wszystkich możliwości jest .

WARIACJE BEZ POWTÓRZEŃ mimo, że nie mają cechy charakterystycznej, to właśnie to je wyróżnia. Inaczej można też zauważyć, że liczy się kolejność wylosowanego podzbioru, ale elementy się nie powtarzają.

Jak widać nawet brak cechy charakterystycznej może być cechą charakterystyczną, jak w wariacjach bez powtórzeń, pod warunkiem, że występuje tylko w tym jednym kombinatorycznym obliczeniu. Spróbujmy zatem zastosować poznaną wiedzę w praktyce. Omówimy zadanie kombinatoryczne z windą, w którym wystąpią wszystkie rodzaje obliczeń kombinatorycznych.

Zadanie 1

Spróbujmy teraz rozwiązać inne zadania z kombinatoryki.

Zadania

Podsumowanie

Jak widać kombinatoryka jest niezbędnym narzędziem rachunku prawdopodobieństwa. Nie obliczymy szansy zajścia bardziej skomplikowanych przypadków bez permutacji, kombinacji czy wariacji.
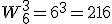